Table of Contents
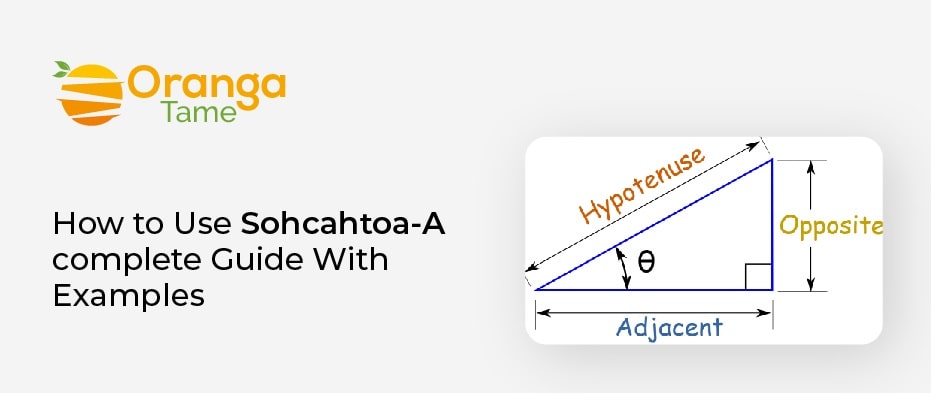
Do you know how to use Sohcahtoa? If not, don’t worry. Here we will explain everything about Soh cah toa. It is a mnemonic device used in mathematics to keep in mind the definitions of the three standard trigonometric functions: Sine, Cosine, and Tangent used to solve the missing sides & angles in a right triangle. They are defined as:
- SOH: Sin()= Opposite/ Hypotenuse
- CAH: Cos(Ɵ)= Adjacent/Hypotenuse
- TOA: Tan(Ɵ)= Opposite/Adjacent
Moreover, we will jump more into the theory as it states that the ratios of the lengths of the two sides of identical right triangles are equal. So, sets of ratios rely on the measure of an acute angle, not on the size of the triangle. However, these ratios allow us to find the missing sides of a right triangle and the missing angles.
What is Sohcahtoa?
Soh cah toa is a worthless mnemonic that helps you keep in mind the definitions of the Sine, Cosine, and Tangent functions. It uses the early letters of Sine, Cosine, and Tangent and the starting letters of the Hypotenuse, opposite and adjacent, to make you remember these trigonometric functions. The trigonometric functions sine, Cosine, and tangent, and their reciprocals are (Cosecant, Secant, and Cotangent). The primary purpose of these ratios is to give an idea of the lengths of the sides of a right triangle that hold an acute angle.
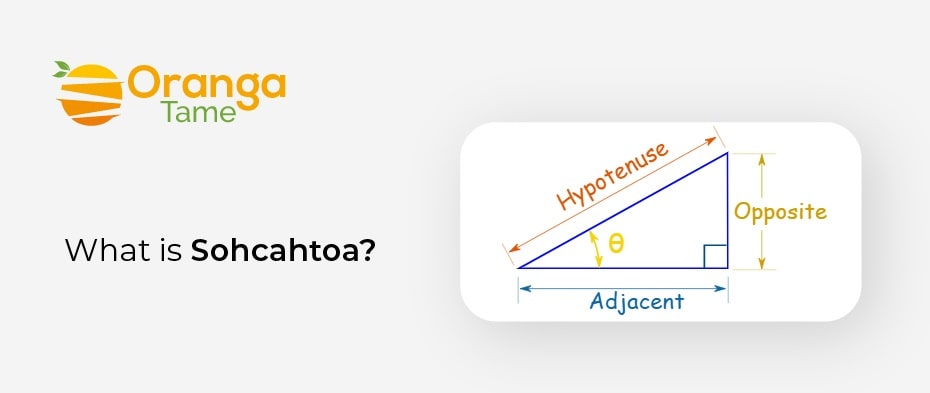
Furthermore, the longest side of the right triangle is the diagonal side known as Hypotenuse. The side refers to 3 units long as the Opposite side & the side with length 4 is known as the Adjacent side. Hense Soh cah toa is the best way to remember the names of these functions.
Soh cah toa is called SOH = sine, which differs from Hypotenuse. CAH: Cosine is adjacent to the Hypotenuse. TOA = Tangent is the inverse of adjacent.
Using Sohcahtoa to Find the Unidentified sides Of the Triangle
So here, we will use trigonometry to work out the unidentified sides of a right-angled triangle through Soh cah toa.
Tag the sides of the right-angle triangle that we have. Then you have to choose the trigonometric ratios. After that, you have to plug the values from the triangle into the function. Then, you just have to calculate the side value.
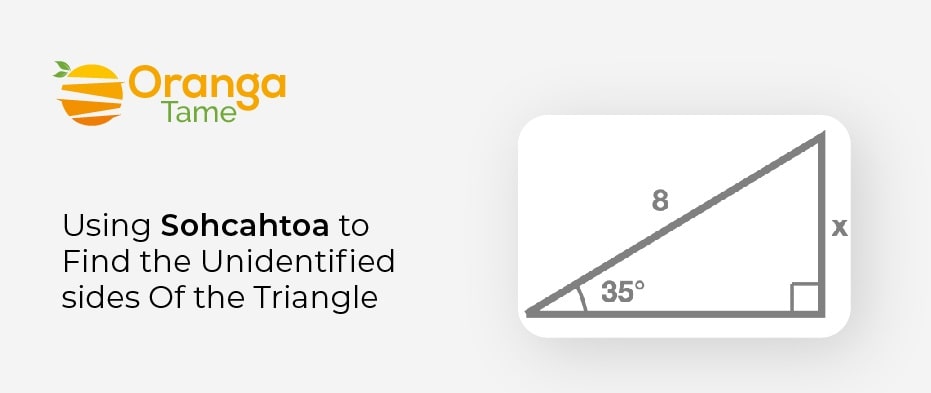
Example 1
However, in a right angle triangle, one leg has a computed of 6 units, and the opposite angle has a calculation of 30 degrees. Now we have to determine the length. So here is the question asked to find the Hypotenuse, sin to find the unidentified length.
SinƟ=
Now we have to substitute the value
Sin30=
0.5=
Now here you have to multiply both sides with
0.5x = x
0.5 = 6
Here you can divide 0.5 into both sides
So here =12, the hypotenuse value is 12 units.
Example 2 by Using Sohcahtoa
An incline is pulled out of the back, so there is a 38 degrees angle between the ramp & the pavement. And the distance from the ramp to the truck is 8 feet. So here, you have to calculate the length of the incline.
So in this problem, we have angle and the adjacent side, so we have to find the Hypotenuse
The given is the angle and adjacent side. So, we are going to solve to get the value of Hypotenuse.
Here, we will use Cosine
CosƟ =
Cos(38) = = = 10.15
So the answer is 10.15 feet
FAQs
- Is Sohcahtoa only applied to right triangles?
Yes, it can only apply to right triangles. If we have any other triangle, we cannot assume the lengths of trigonometric ratios. There are other methods we will learn more in Maths analysis and in other laws to handle such cases.
- When & why do we use Soh cah toa?
We can use it when we have a right angle whose sides lengths are given, and you have to find the other side of the triangle.
Final Thoughts
Finally, we will say that Soh cah toa helps remember the name of the most familiar trigonometric functions, which are SinƟ, CosƟ, and tanƟ and their inverse (Cosec, Secant, and Secant, and cotangent). Moreover, it help find the unknown side and the missing angle of the right-angle triangle. I hope you all understand about Sohcahtoa. If you have any queries related to the topic, comment to us.